Hierarchical Deterministic Wallets in ProtectToolkit

Bitcoin Improvement Protocol 0032 (BIP32) introduced Hierarchical Deterministic Wallets, which use elliptic curve mathematics to calculate multiple key pair chains from a single root. This eliminates the need for backups after each Bitcoin transaction, by allowing you to create a new public address for each transaction or group of transactions without knowing the private key.

For a full description of BIP32 HD wallets, see https://github.com/bitcoin/bips/blob/master/bip-0032.mediawiki.

BIP32 Implementation in ProtectToolkit

ProtectToolkit introduced support for BIP32 in release 5.4. ProtectToolkit generates HD wallets as PKCS#11 keypairs within the ProtectServer HSM, using the custom algorithms CKM_BIP32_MASTER_DERIVE and CKM_BIP32_CHILD_DERIVE. While public keys can be exported in plaintext, the ProtectServer security architecture prevents the plaintext base58 value of private keys from existing outside of the HSM.

This information is encoded in the key's custom attributes as described below.

Validating BIP32 Test Vectors With ProtectServer

For testing purposes, you can use the procedure below to confirm that BIP32 key generation is functioning properly. The BIP32 test vectors are located at https://github.com/bitcoin/bips/blob/master/bip-0032.mediawiki#test-vectors.

Descriptions of the attributes described below can be found at https://github.com/bitcoin/bips/blob/master/bip-0032.mediawiki#serialization-format.

To validate BIP32 test vectors with ProtectServer

1.Generate a BIP32 master keypair, specifying the seed provided in one of the test vectors (example: Test Vector 1). If you want to confirm the private key, you must set CKA_SENSITIVE=0 during key creation.

Example seed (hexadecimal): 000102030405060708090a0b0c0d0e0f

2.Examine the following key attribute fields (you can also use C_GetAttribute to obtain these values):

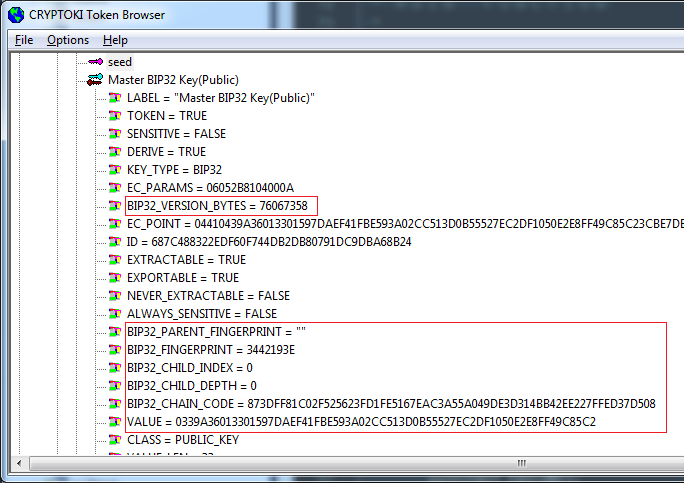
a.BIP32_VERSION_BYTES=<4_bytes>

This attribute will have one of four values. It is provided in integer form. Convert it to hexadecimal as follows:

Key Type	Decimal	Hexadecimal
Mainnet Public Key	76067358	0488B21E
Mainnet Private Key	76066276	0488ADE4
Testnet Public Key	70617039	043587CF
Testnet Private Key	70615956	04358394

b.BIP32_CHILD_DEPTH=<1_byte>

Represents the depth of derivations from the master key (00 on the master node).

c.BIP32_PARENT_FINGERPRINT=<4_bytes>

If this is the master key, the field appears empty. The correct value is 00000000.

d.BIP32_CHILD_INDEX=<4_bytes>

If necessary, append zeroes to include the full 4 bytes. In this example, the correct value is 00000000.

e.BIP32_CHAIN_CODE=<32_bytes>

f.VALUE=<32_bytes>

The key value in hexadecimal form. This attribute field is only visible if SENSITIVE=0.

3.Concatenate these values, in the above order, into a string.

0488B21E000000000000000000873DFF81C02F525623FD1FE5167EAC3A55A049DE3D314BB42EE227FFED37D5080339A36013301597DAEF41FBE593A02CC513D0B55527EC2DF1050E2E8FF49C85C2

4.Hash the string twice with SHA-256 to obtain the checksum.

AB473B21

5.Append the checksum to the end of the original string.

0488B21E000000000000000000873DFF81C02F525623FD1FE5167EAC3A55A049DE3D314BB42EE227FFED37D5080339A36013301597DAEF41FBE593A02CC513D0B55527EC2DF1050E2E8FF49C85C2AB473B21

6.Convert the entire string from hexadecimal to base58.

xpub661MyMwAqRbcFtXgS5sYJABqqG9YLmC4Q1Rdap9gSE8NqtwybGhePY2gZ29ESFjqJoCu1Rupje8YtGqsefD265TMg7usUDFdp6W1EGMcet8

7.Compare the base58 value to the expected value from the BIP32 test vector.